How to use these HTML slides

• Use the cursor keys left/right to navigate through the slides
• Click page number (bottom right) to open navigation menu
• Press f/ESC to enter/leave fullscreen mode
• Press o or ESC to enter/leave overview mode
• Double-click an item (e.g. an image) to zoom in/out.

Interactive Demo Applications

• The demos are written in C++ using the PMP library
• They are cross-compiled to Javascript using emscripten
• They require support for WebGL 2
  • See https://caniuse.com/webgl2
  • The demos work nicely on Chrome, Chromium, or Firefox
  • They do not run on Apple Safari in MacOS and iOS

Loop Subdivision

• Subdivision scheme for triangle meshes
  
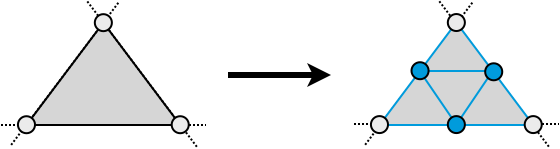
• Generates \(C^2\) continuous limit surfaces:
  • \(C^1\) for extraordinary vertices (valence ≠ 6)
  • \(C^2\) continuous everywhere else

Loop, Smooth Subdivision Surfaces Based on Triangles, M.S. thesis, 1987

Loop Subdivision Rules

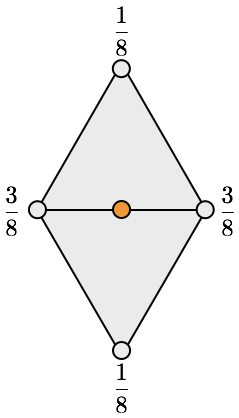
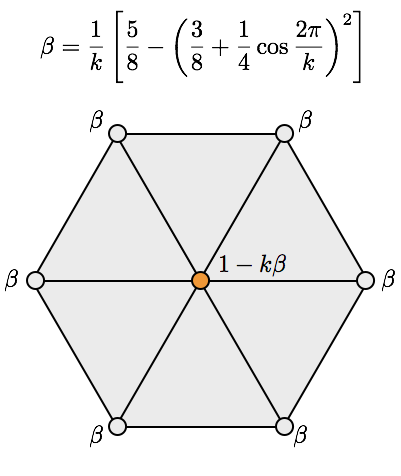
Loop, Smooth Subdivision Surfaces Based on Triangles, M.S. thesis, 1987

Generalized Catmull-Clark Subdivision

• Subdivision scheme for arbitrary polygons
  
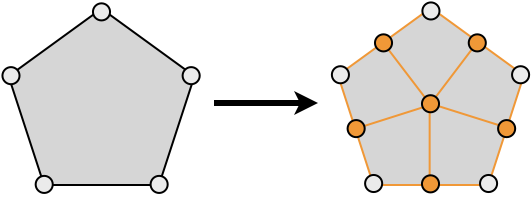
• Connect new face points to edge-vertex-edge triple
  • Turns all polygon faces into quads
• Generates \(C^2\) continuous limit surfaces:
  • \(C^1\) for extraordinary vertices (valence ≠ 4)
  • \(C^2\) continuous everywhere else

DeRose et al, Subdivision Surfaces in Character Animation, SIGGRAPH 1998

Catmull-Clark Rules

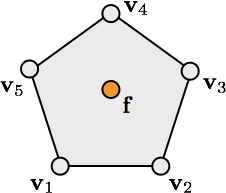
\[\vec{f} = \frac{1}{n} \sum_{i=1}^n \vec{v}_i\]

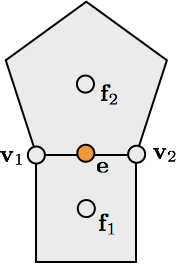
\[\vec{e} = \frac{1}{4} \left(\vec{v}_1 + \vec{v}_2 + \vec{f}_1 + \vec{f}_2\right)\]

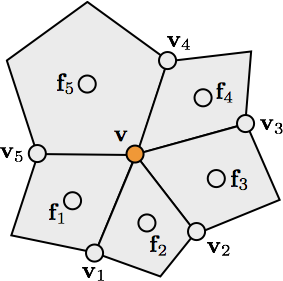
\[ \vec{v} = \frac{k-2}{k} \vec{v} + \frac{1}{k^2} \sum_{i=1}^k \vec{v}_i + \frac{1}{k^2} \sum_{i=1}^k \vec{f}_i \]

DeRose et al, Subdivision Surfaces in Character Animation, SIGGRAPH 1998

Try it yourself!

Try it yourself!

Model created using Blender, original from Willem-Paul van Overbruggen

Diffusion Flow on Meshes

• Continuous PDE: \(\frac{\partial \vec{x}}{\partial t} \;=\; \lambda \Delta \vec{x}\)
• Explicit integration per vertex: \(\vec{x}_i \leftarrow \vec{x}_i + \delta t \, \lambda \Delta \vec{x}_i\)

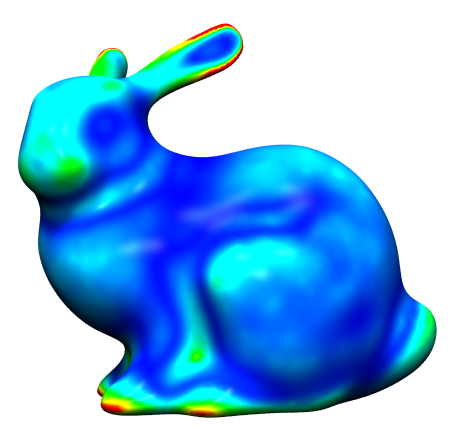
Uniform Laplace Discretization

\[ \laplace \vec{x}\of{v_i} \;:=\; \frac{1}{\abs{\set{N}_1\of{v_i}}} \sum_{v_j \in \set{N}_1\of{v_i}} \left( \vec{x}\of{v_j} - \vec{x}\of{v_i} \right) \]

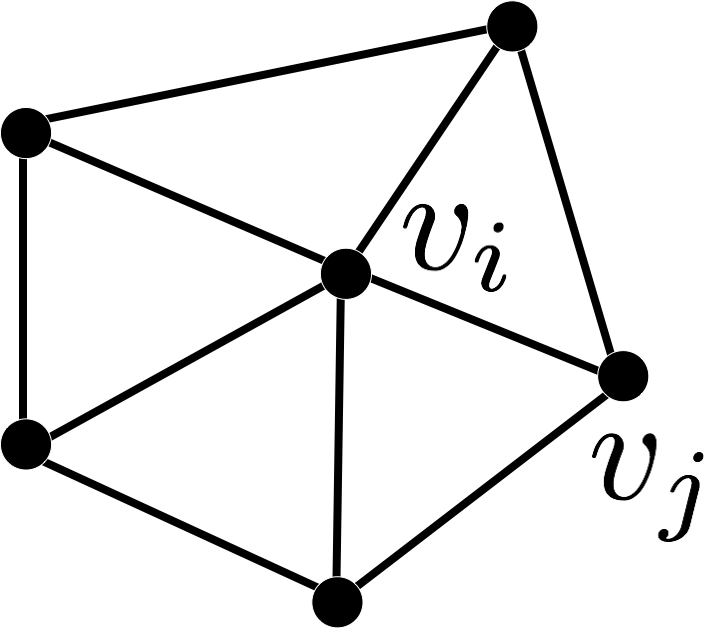
Taubin, A Signal Processing Approach to Fair Surface Design, SIGGRAPH 1995

Cotan Laplace Discretization

\[ \laplace \vec{x}\of{v_i} \;:=\; \frac{1}{2A\of{v_i}} \sum_{v_j \in \set{N}_1\of{v_i}} \left( \cot \alpha_{ij} + \cot \beta_{ij} \right) \left( \vec{x}\of{v_j} - \vec{x}\of{v_i} \right) \]

Meyer et al, Discrete Differential-Geometry Operators for Triangulated 2-Manifolds, VisMath III, 2003

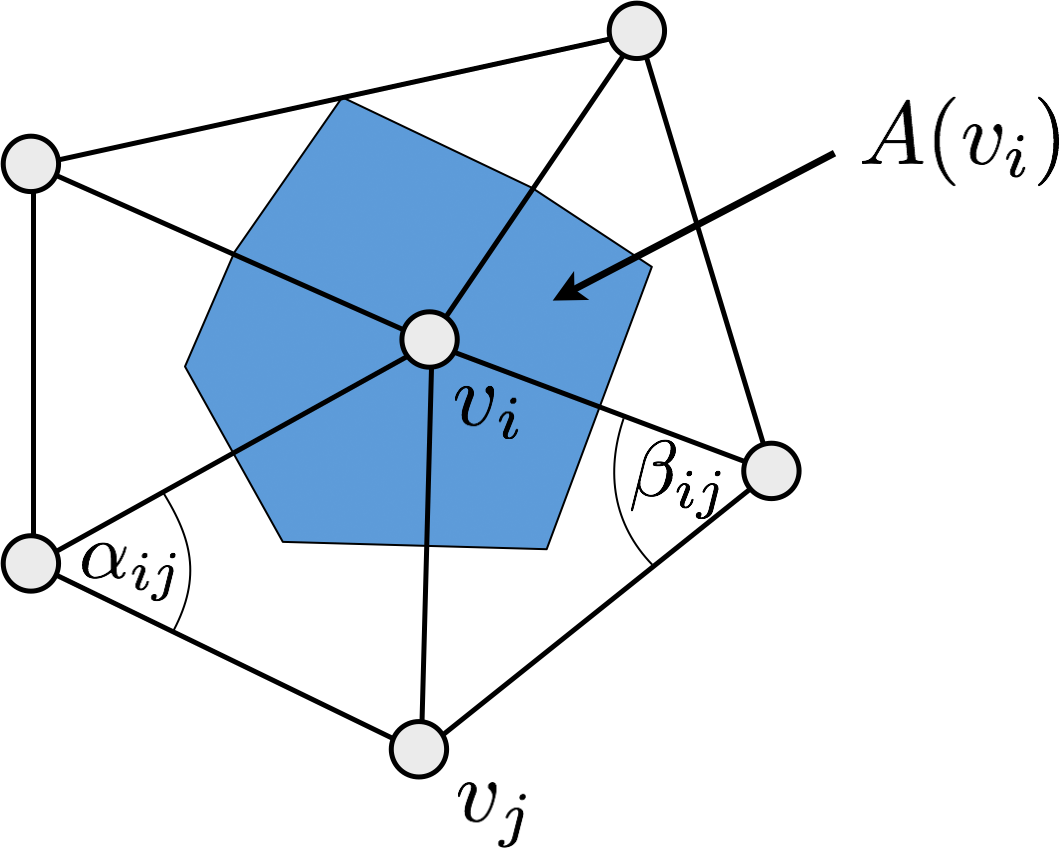
Uniform or Cotan Discretization?

Desbrun et al, Implicit Fairing of Irregular Meshes using Diffusion and Curvature Flow, SIGGRAPH 1999

Numerical Integration

• Let’s write the position update in matrix notation
• Write all points \(\vec{x}_i^{(t)}\) in a large vector/matrix: \[\vec{X}^{(t)} = \trans{\left( \vec{x}_1^{(t)}, \ldots, \vec{x}_n^{(t)} \right)} \in \R^{n\times 3}\]
• Matrix version of explicit integration \[\vec{X}^{(t+1)} = (\vec{I} + \delta t \, \lambda \vec{L}) \, \vec{X}^{(t)}\]
• Matrix version of implicit integration \[(\vec{I} - \delta t \, \lambda \vec{L}) \, \vec{X}^{(t+1)} = \vec{X}^{(t)}\]

Desbrun et al, Implicit Fairing of Irregular Meshes using Diffusion and Curvature Flow, SIGGRAPH 1999

Try it yourself!

Isotropic Triangle Remeshing

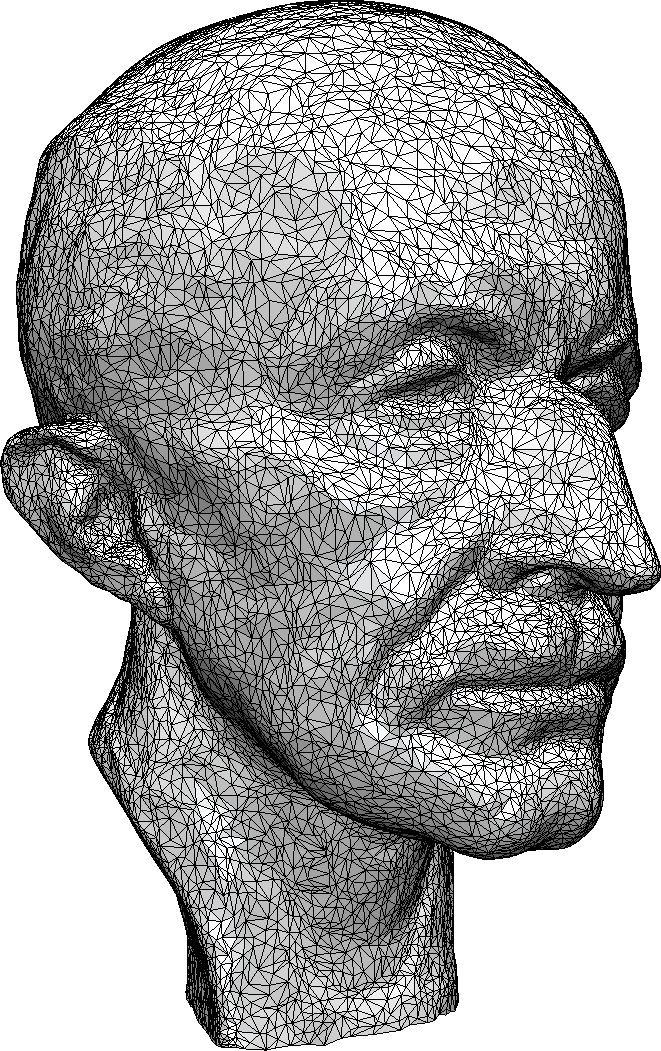
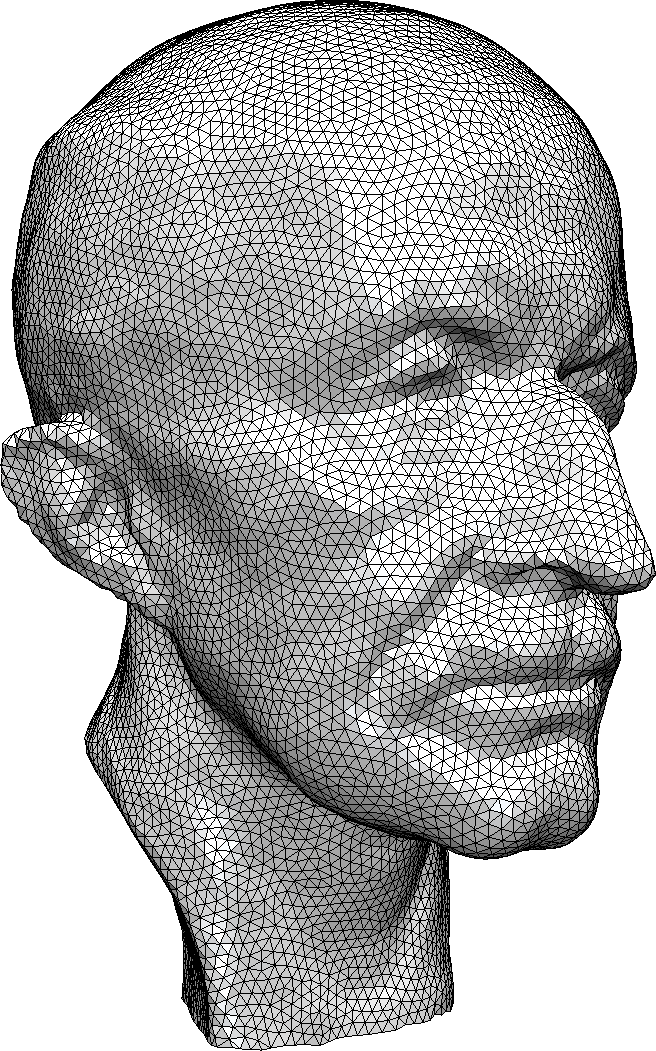
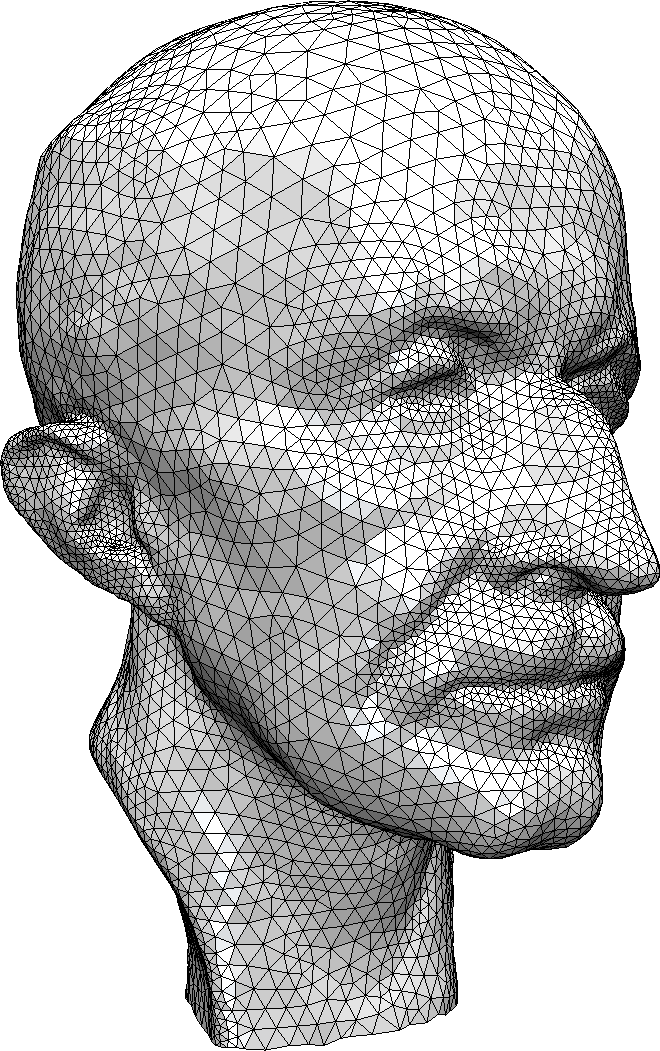
Uniform Remeshing

• Specify target edge length \(L\)
• Iterate a few times
  1. Split edges longer than \(\frac{4}{3} L\)
  2. Collapse edges shorter than \(\frac{4}{5}L\)
  3. Flip edges to get closer to valence 6
  4. Shift vertices by tangential relaxation
  5. Project vertices onto input mesh

Botsch & Kobbelt, A Remeshing Approach to Multiresolution Modeling, SGP 2004

Local Remeshing Operators

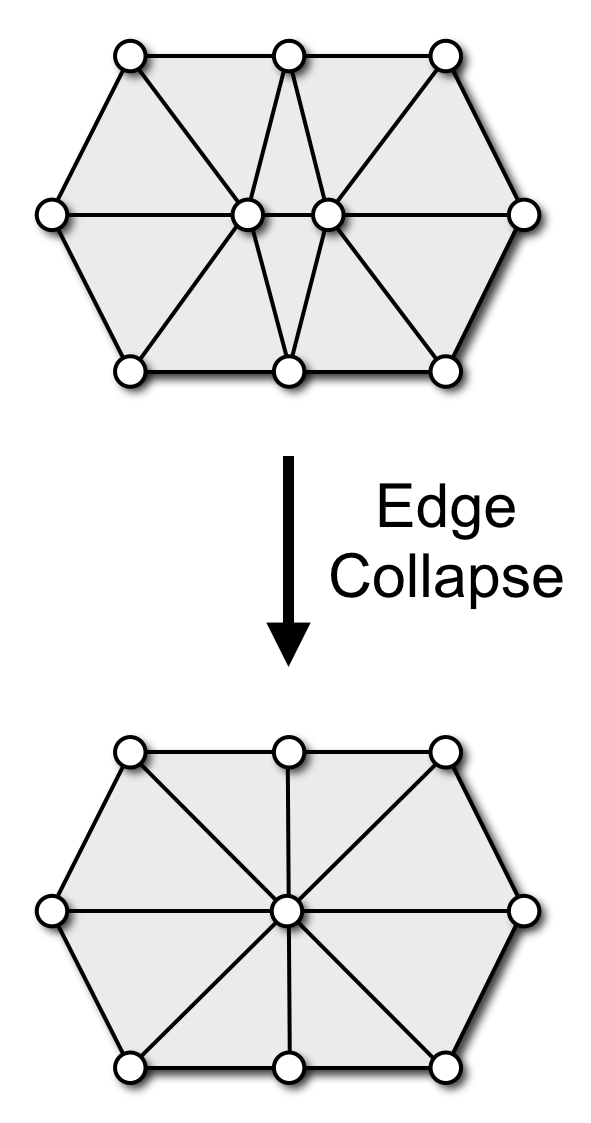
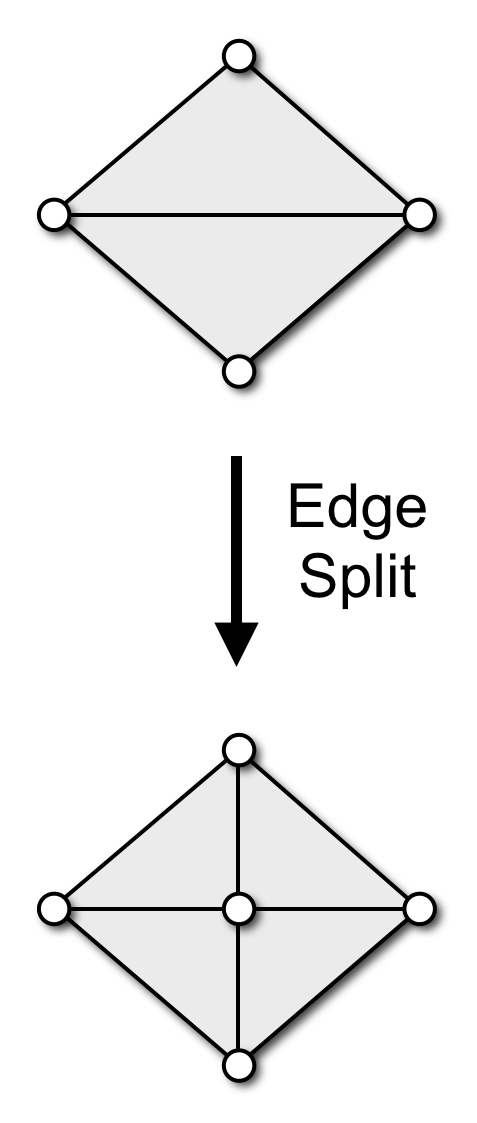
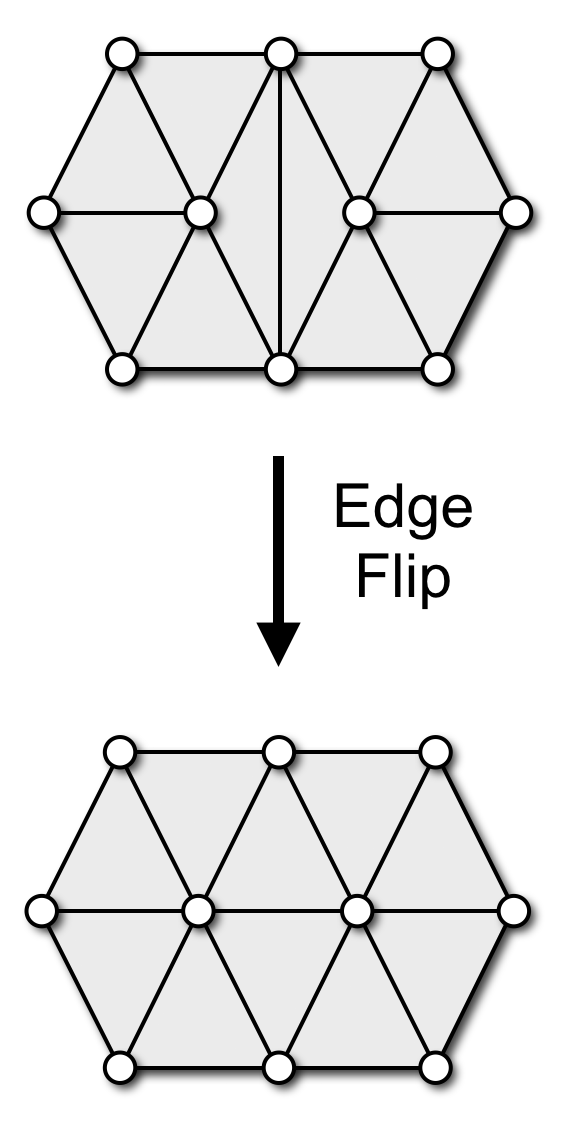
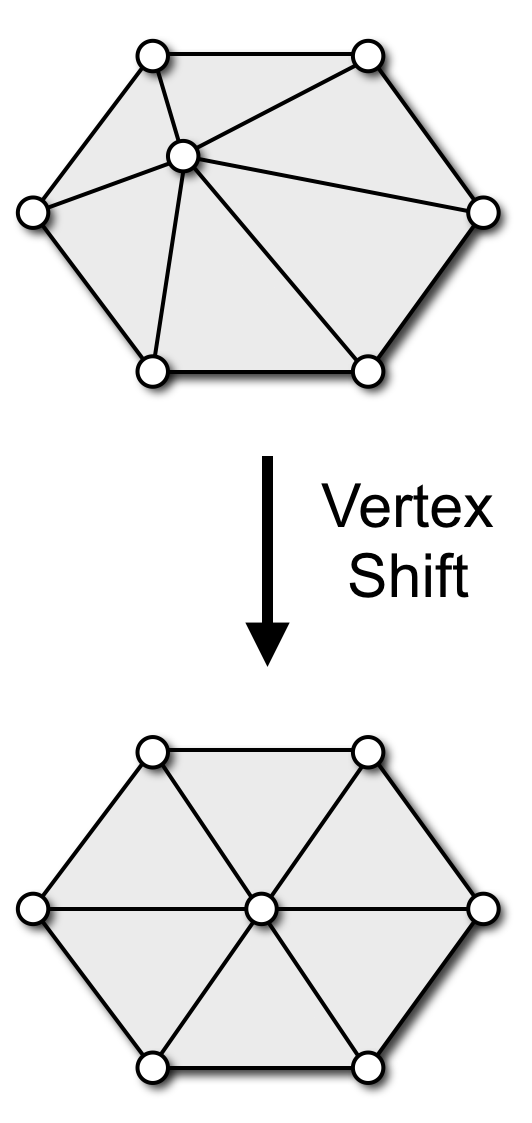
Botsch & Kobbelt, A Remeshing Approach to Multiresolution Modeling, SGP 2004

Adaptive Remeshing

Dunyach et al, Adaptive Remeshing for Real-Time Mesh Deformation, EG 2013

Real-Time Remeshing

Dunyach et al, Adaptive Remeshing for Real-Time Mesh Deformation, EG 2013

Real-Time Remeshing

Dunyach et al, Adaptive Remeshing for Real-Time Mesh Deformation, EG 2013

Let’s try!

Feature Preservation

Let’s try!